Menguasai Seni Menyederhanakan Pecahan: Panduan Lengkap dengan Contoh Soal Kelas 4

Pecahan adalah konsep matematika dasar yang penting untuk dipahami. Mereka mewakili sebagian dari keseluruhan dan seringkali muncul dalam kehidupan sehari-hari, mulai dari membagi pizza hingga menghitung bahan-bahan dalam resep. Bagi siswa kelas 4, memahami dan mampu menyederhanakan pecahan adalah langkah krusial untuk membangun fondasi yang kuat dalam matematika. Artikel ini akan membahas secara mendalam tentang cara menyederhanakan pecahan, dilengkapi dengan contoh soal yang relevan untuk siswa kelas 4, serta tips dan trik untuk memudahkan pemahaman.

Apa Itu Menyederhanakan Pecahan?

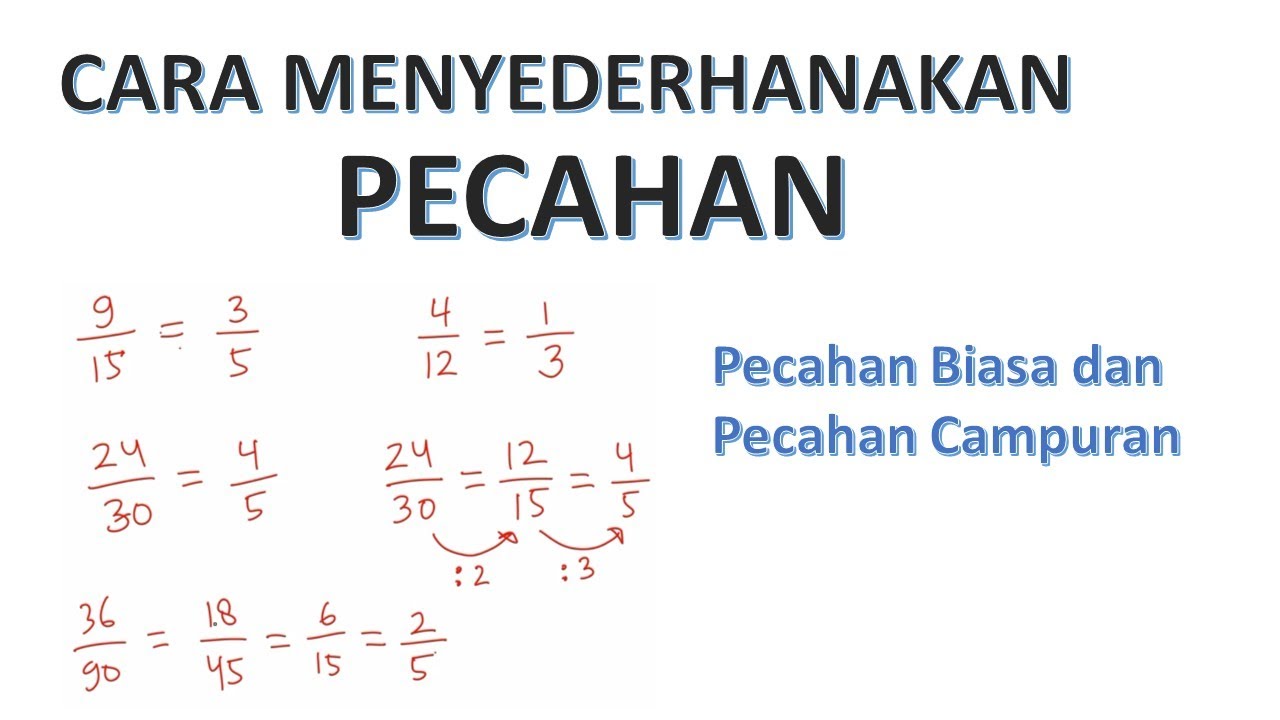
Menyederhanakan pecahan berarti menulis pecahan dalam bentuk yang paling sederhana, tanpa mengubah nilainya. Bentuk paling sederhana ini diperoleh ketika pembilang (angka di atas garis pecahan) dan penyebut (angka di bawah garis pecahan) tidak memiliki faktor persekutuan selain 1. Dengan kata lain, tidak ada angka yang dapat membagi habis baik pembilang maupun penyebut secara bersamaan.

Mengapa Menyederhanakan Pecahan Penting?

Ada beberapa alasan mengapa penting untuk menyederhanakan pecahan:

• Memudahkan Pemahaman: Pecahan yang disederhanakan lebih mudah dipahami dan dibandingkan dengan pecahan lainnya.
• Mempermudah Perhitungan: Melakukan operasi matematika (penjumlahan, pengurangan, perkalian, dan pembagian) dengan pecahan yang disederhanakan akan jauh lebih mudah.
• Standar dalam Matematika: Dalam banyak kasus, jawaban akhir dalam soal matematika harus disajikan dalam bentuk pecahan yang paling sederhana.
• Aplikasi dalam Kehidupan Sehari-hari: Memahami pecahan yang disederhanakan membantu dalam menyelesaikan masalah praktis sehari-hari, seperti membagi makanan atau mengukur bahan.

Cara Menyederhanakan Pecahan: Mencari Faktor Persekutuan Terbesar (FPB)

Metode utama untuk menyederhanakan pecahan adalah dengan mencari Faktor Persekutuan Terbesar (FPB) dari pembilang dan penyebut. FPB adalah angka terbesar yang dapat membagi habis kedua angka tersebut. Berikut adalah langkah-langkahnya:

1. Tentukan Faktor dari Pembilang dan Penyebut:

   • Faktor adalah angka yang dapat membagi habis suatu angka tanpa sisa.
   • Contoh: Faktor dari 12 adalah 1, 2, 3, 4, 6, dan 12. Faktor dari 18 adalah 1, 2, 3, 6, 9, dan 18.

2. Cari Faktor Persekutuan:

   • Faktor persekutuan adalah faktor yang dimiliki bersama oleh pembilang dan penyebut.
   • Contoh: Faktor persekutuan dari 12 dan 18 adalah 1, 2, 3, dan 6.

3. Tentukan Faktor Persekutuan Terbesar (FPB):

   • FPB adalah faktor persekutuan terbesar di antara semua faktor persekutuan.
   • Contoh: FPB dari 12 dan 18 adalah 6.

4. Bagi Pembilang dan Penyebut dengan FPB:

   • Setelah menemukan FPB, bagi pembilang dan penyebut dengan FPB tersebut.
   • Contoh: Untuk menyederhanakan pecahan 12/18, bagi pembilang (12) dan penyebut (18) dengan FPB (6): 12 ÷ 6 = 2 dan 18 ÷ 6 = 3. Jadi, bentuk sederhana dari 12/18 adalah 2/3.

Contoh Soal dan Pembahasan (Kelas 4)

Berikut adalah beberapa contoh soal menyederhanakan pecahan yang cocok untuk siswa kelas 4, beserta pembahasannya langkah demi langkah:

Soal 1: Sederhanakan pecahan 6/8.

• Langkah 1: Tentukan faktor dari pembilang (6) dan penyebut (8).
  • Faktor dari 6: 1, 2, 3, 6
  • Faktor dari 8: 1, 2, 4, 8
• Langkah 2: Cari faktor persekutuan.
  • Faktor persekutuan dari 6 dan 8: 1, 2
• Langkah 3: Tentukan FPB.
  • FPB dari 6 dan 8: 2
• Langkah 4: Bagi pembilang dan penyebut dengan FPB.
  • 6 ÷ 2 = 3
  • 8 ÷ 2 = 4
• Jawaban: Bentuk sederhana dari 6/8 adalah 3/4.

Soal 2: Sederhanakan pecahan 9/12.

• Langkah 1: Tentukan faktor dari pembilang (9) dan penyebut (12).
  • Faktor dari 9: 1, 3, 9
  • Faktor dari 12: 1, 2, 3, 4, 6, 12
• Langkah 2: Cari faktor persekutuan.
  • Faktor persekutuan dari 9 dan 12: 1, 3
• Langkah 3: Tentukan FPB.
  • FPB dari 9 dan 12: 3
• Langkah 4: Bagi pembilang dan penyebut dengan FPB.
  • 9 ÷ 3 = 3
  • 12 ÷ 3 = 4
• Jawaban: Bentuk sederhana dari 9/12 adalah 3/4.

Soal 3: Sederhanakan pecahan 10/15.

• Langkah 1: Tentukan faktor dari pembilang (10) dan penyebut (15).
  • Faktor dari 10: 1, 2, 5, 10
  • Faktor dari 15: 1, 3, 5, 15
• Langkah 2: Cari faktor persekutuan.
  • Faktor persekutuan dari 10 dan 15: 1, 5
• Langkah 3: Tentukan FPB.
  • FPB dari 10 dan 15: 5
• Langkah 4: Bagi pembilang dan penyebut dengan FPB.
  • 10 ÷ 5 = 2
  • 15 ÷ 5 = 3
• Jawaban: Bentuk sederhana dari 10/15 adalah 2/3.

Soal 4: Sederhanakan pecahan 14/21.

• Langkah 1: Tentukan faktor dari pembilang (14) dan penyebut (21).
  • Faktor dari 14: 1, 2, 7, 14
  • Faktor dari 21: 1, 3, 7, 21
• Langkah 2: Cari faktor persekutuan.
  • Faktor persekutuan dari 14 dan 21: 1, 7
• Langkah 3: Tentukan FPB.
  • FPB dari 14 dan 21: 7
• Langkah 4: Bagi pembilang dan penyebut dengan FPB.
  • 14 ÷ 7 = 2
  • 21 ÷ 7 = 3
• Jawaban: Bentuk sederhana dari 14/21 adalah 2/3.

Soal 5: Sederhanakan pecahan 16/24.

• Langkah 1: Tentukan faktor dari pembilang (16) dan penyebut (24).
  • Faktor dari 16: 1, 2, 4, 8, 16
  • Faktor dari 24: 1, 2, 3, 4, 6, 8, 12, 24
• Langkah 2: Cari faktor persekutuan.
  • Faktor persekutuan dari 16 dan 24: 1, 2, 4, 8
• Langkah 3: Tentukan FPB.
  • FPB dari 16 dan 24: 8
• Langkah 4: Bagi pembilang dan penyebut dengan FPB.
  • 16 ÷ 8 = 2
  • 24 ÷ 8 = 3
• Jawaban: Bentuk sederhana dari 16/24 adalah 2/3.

Tips dan Trik untuk Menyederhanakan Pecahan:

• Gunakan Tabel Perkalian: Tabel perkalian dapat membantu siswa mengidentifikasi faktor dengan cepat.
• Mulai dengan Angka Kecil: Jika Anda tidak yakin dengan FPB, coba bagi pembilang dan penyebut dengan angka kecil seperti 2, 3, atau 5 terlebih dahulu. Jika keduanya habis dibagi, lanjutkan dengan angka yang lebih besar.
• Perhatikan Angka Genap dan Ganjil: Jika pembilang dan penyebut keduanya genap, maka keduanya pasti dapat dibagi dengan 2.
• Latihan Secara Teratur: Semakin banyak siswa berlatih, semakin mudah mereka memahami dan menguasai konsep menyederhanakan pecahan.
• Visualisasikan Pecahan: Gunakan diagram atau gambar untuk membantu siswa memahami konsep pecahan dan bagaimana menyederhanakannya. Misalnya, gambarlah lingkaran yang dibagi menjadi beberapa bagian dan arsir sebagian untuk mewakili pecahan.

Kesalahan Umum yang Harus Dihindari:

• Tidak Mencari FPB Terbesar: Terkadang siswa menemukan faktor persekutuan tetapi bukan yang terbesar. Ini akan menghasilkan pecahan yang belum sepenuhnya disederhanakan.
• Hanya Membagi Pembilang atau Penyebut: Pastikan untuk membagi baik pembilang maupun penyebut dengan angka yang sama.
• Salah Menentukan Faktor: Ketelitian dalam menentukan faktor sangat penting untuk menemukan FPB yang tepat.

Kesimpulan

Menyederhanakan pecahan adalah keterampilan matematika penting yang perlu dikuasai oleh siswa kelas 4. Dengan memahami konsep FPB dan berlatih secara teratur, siswa dapat dengan mudah menyederhanakan pecahan dan membangun fondasi yang kuat untuk konsep matematika yang lebih kompleks di masa depan. Dengan panduan lengkap ini dan contoh soal yang relevan, diharapkan siswa kelas 4 dapat menguasai seni menyederhanakan pecahan dan menerapkannya dalam berbagai situasi. Ingatlah, kunci utama adalah latihan dan pemahaman konsep dasar!